DISTRIBUCIÓN BINOMIAL
EJERCICIOS BINOMIAL
Formula de la distribución binomial
Ejemplo 1:
Imaginemos que un 80% de personas en el mundo ha visto el partido de la final del último mundial de fútbol. Tras el evento, 4 amigos se reúnen a conversar, ¿Cuál es la probabilidad de que 3 de ellos hayan visto el partido?
Definamos las variables del experimento:
n = 4 (es el total de la muestra que tenemos)
x = número de éxitos, que en este caso es igual a 3, dado que buscamos la probabilidad de que 3 de los 4 amigos lo hayan visto.
p = probabilidad de éxito (0,8)
q = probabilidad de fracaso (0,2). Este resultado se obtiene al restar 1-p.
Tras definir todas nuestras variables, simplemente sustituimos en la formula.
Hay una probabilidad del 40,96% de que 3 de los 4 amigos haya visto el partido de la final del mundial.
Ejemplo 2:
De todas las flores plantadas por una empresa de jardinería, el 90% sobrevive. Si se plantan 10 flores ¿cuál es la probabilidad de que 9 o más sobrevivan?
Solución:
Antes de aplicar la fórmula, verificamos que se trate de un experimento binomial. Para ello, tiene que cumplir con las 4 condiciones que mencionamos arriba. Efectivamente, se trata de un experimento binomial.
En este caso, vamos a centrarnos en las flores que sobreviven, por ello diremos que:
Entonces consideramos un éxito si la flor sobrevive. A las que flores que se mueren, las consideramos como un fracaso.
Aplicaremos la fórmula binomial:
Nos piden calcular la probabilidad de 9 o más sobrevivan.
Este problema tiene trampa, porque dado que se plantaron 10 flores, la máxima cantidad de flores que pueden sobrevivir es 10, por lo tanto:
Ahora colocamos los valores de n, k y p. Recuerda que n es el número de ensayos, k el número de éxitos y p la probabilidad de éxito. En este caso:
Vamos a calcular cada probabilidad por separado, empezando con P(X = 9):
Continuamos con P(X = 10).
La probabilidad de que 9 o más sobrevivan es del 73.61%
Ejeplo 3:
Si de seis a siete de la tarde se admite que un número de teléfono de
cada cinco está comunicando.
¿Cuál es la probabilidad de que, cuando se marquen 10 números de
teléfono elegidos al azar, sólo comuniquen dos?
La probabilidad de que 2 telefonos se comuniquen es del 30.20%
Ejemplo 4:
Ejemplo 5:
REFERENCIAS BIBLIOGRÁFICAS
-Condiciones que debe cumplir la distribucion binomial [en línea]. [Fecha de consulta: 8 de diciembre del 2020].Disponible en :
https://economipedia.com/definiciones/distribucion-binomial.html
-Qué significa distribución binomial en Matemáticas [en línea]. [Fecha de consulta: 8 de diciembre del 2020].Disponible en :
https://www3.uji.es/~mateu/t4-alumnos.pdf
-Distribución binomial, ejercicios resueltos [en línea]. [Fecha de consulta: 8 de diciembre del 2020].Disponible en :
https://matemovil.com/distribucion-binomial-ejercicios-resueltos/
-BINOMIAL Ejercicios resueltos [en línea]. [Fecha de consulta: 8 de diciembre del 2020].Disponible en :
https://calculo.cc/temas/temas_estadistica/binomial_normal/problemas/prob_binomial1.html















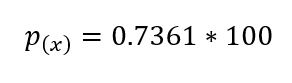









Comentarios
Publicar un comentario