PROBABILIDADES
La probabilidad es el cálculo matemático que evalúa las posibilidades que existen de que una cosa suceda cuando interviene el azar.
EXPERIMENTO ALEATORIO
Consiste en repetir un fenómeno aleatorio con el objetivo de analizarlo y extraer conclusiones sobre su comportamiento.
De la definicion se puede deducir que se trata del estudio de situaciones dominadas por las leyes del azar.
No siempre que tratemos de realizar un experimento aleatorio, vamos a poder experimentar de forma tangible. Por ejemplo, imaginemos que queremos estudiar el comportamiento de una moneda. La moneda es tangible, la podemos ver y tocar. Lanzarla y comprobar el resultado (cara o cruz) nos corresponde a nosotros. Ahora, supongamos el ejemplo del clima. No podemos mover las nubes o cambiar las temperaturas. Al menos de forma tangible.
ESPACIO MUESTRAL
El espacio muestral está formado por todos los posibles resultados de un experimento aleatorio. Es decir, se compone de todos y cada uno de los sucesos elementales.
El espacio muestral es una parte del espacio probabilístico. Como su propio nombre indica, está formado por los elementos de la muestra. Al contrario, el espacio probabilístico engloba todos los elementos. Incluso aunque no salgan recogidos en la muestra.
Ejemplo 1:
-El espacio muestral del lanzamiento de una moneda es:
E={cara,cruz}
ya que éstas son las dos únicas posibilidades.
Ejemplo 2:
-El espacio muestral del lanzamiento de un dado es:
E={1,2,3,4,5,6}
pero también puede ser
E={par,impar}
EJEMPLOS DE PROBABILIDADES DE : SUMA Y MULTIPLICACIÓN
* Regla de la Suma
La regla de adición o regla de la suma, establece que si tenemos un evento A y un evento B, la probabilidad de que ocurra el evento A o el evento B se calcula de la siguiente manera:
Donde:
P(A) : probabilidad de que ocurra el evento A.
P(B) : probabilidad de que ocurra el evento B.
P(A⋃B) : probabilidad de que ocurra el evento A o el evento B.
P(A⋂B) : probabilidad de que ocurra el evento A y el evento B a la vez.
Ejemplo 1:
La probabilidad de que un día cualquiera, Carlos almuerce pollo frito es de 0,4. La probabilidad de que almuerce hamburguesa es de 0,3; mientras que la probabilidad de que almuerce pollo frito y hamburguesa el mismo día es de 0,1. Calcula la probabilidad de que un día cualquiera, Carlos almuerce pollo frito o hamburguesa.
Solución:
Definimos nuestras probabilidades:
- Probabilidad de que Carlos almuerce pollo frito: P(A) = 0,4.
- Probabilidad de que Carlos almuerce hamburguesa: P(B) = 0,3.
- Probabilidad de que Carlos almuerce pollo frito y hamburguesa el mismo día: P(A⋂B) = 0,1.
- Probabilidad de que Carlos almuerce pollo frito o hamburguesa:
- P(A⋃B) = ?
Ahora, aplicamos nuestra fórmula:
Ejemplo 2:
La probabilidad de que al tirar un dado, salga 1, es de 1/6. La probabilidad de que salga 3, es de 1/6. Calcular la probabilidad de que al tirar un dado, salga 1 o 3.
Solución:
Definimos nuestros eventos:
- Probabilidad de que salga 1: P(A) = 1/6.
- Probabilidad de que salga 3: P(B) = 1/6.
- Probabilidad de que salga 1 y 3 al mismo tiempo P(A⋂B) = 0. Este valor es cero, dado que son eventos mutuamente excluyentes. Si sale 1, ya no puede salir 3.
- Probabilidad de que salga 1 o 3: P(A⋃B) = ?
Ahora, aplicamos nuestra fórmula:
* Regla de la Multiplicación
La regla de la multiplicación o regla del producto, permite encontrar la probabilidad de que ocurra el evento A y el evento B al mismo tiempo (probabilidad conjunta). Esta regla depende de si los eventos son dependientes o independientes.
Eventos dependientes
Dos eventos A y B son dependientes, si la ocurrencia de uno de ellos afecta la ocurrencia del otro. Para eventos dependientes, la regla de la multiplicación establece que:
EJEMPLO :
Una caja contiene 2 canicas azules y 3 rojas. Si se extraen dos canicas al azar sin reposición, ¿cuál es la probabilidad de que las dos sean azules?
Solución:
Dado que las canicas serán extraídas de la misma caja, y que las canicas que se extraigan, no serán devueltas a la caja (no hay reposición), entonces, se trata de eventos dependientes.
- Evento A: obtener una canica azul en la primera extracción.
- Evento B: obtener una canica azul en la segunda extracción.
Por la regla de la multiplicación, sabemos que:
Eventos independientes
Dos eventos A y B son independientes, si la ocurrencia de uno de ellos no afecta la ocurrencia del otro, es decir, cuando los eventos A y B no están relacionados. Para eventos independientes, la regla de la multiplicación establece que:
Esto se debe, a que en los eventos independientes, la ocurrencia de un evento, no afecta a la ocurrencia del otro:
Ejemplo:
En un colegio, la probabilidad de que un alumno seleccionado al azar hable inglés es de 0,20; mientras que la probabilidad de que un alumno juegue fútbol es de 0,80.
El hecho de que un alumno hable inglés, no afecta en nada que juegue fútbol; por lo tanto, se trata de eventos independientes.
- Evento A: que el alumno hable inglés. P(A) = 0,20.
- Evento B: que el alumno juegue fútbol. P(B) = 0,80.
Usamos la regla de la multiplicación para eventos independientes:
REFERENCIAS BIBLIOGRÁFICAS
- EXPERIMENTO ALEATORIO [en línea]. [Fecha de consulta: 3 de noviembre del 2020].Disponible en :
https://economipedia.com/definiciones/experimento-aleatorio.html
- ESPACIO MUESTRAL [en línea]. [Fecha de consulta: 3 de noviembre del 2020].Disponible en :
https://economipedia.com/definiciones/espacio-muestral.html
- PROBABILIDADADES:REGLA DE MULTIPLICACIÓN [en línea]. [Fecha de consulta: 3 de noviembre del 2020]. Disponible en:
https://www.youtube.com/watch?v=S7W5Tlpa3mA
- REGLA DE LA MULTIPLICACIÓN O PRODUCTO DE PROBABILIDADES [en línea]. [Fecha de consulta:3 de noviembre del 2020]. Disponible en:
https://matemovil.com/regla-de-la-multiplicacion-o-producto-de-probabilidades/
- CONCEPTOS BÁSICOS DE PROBABILIDAD [en línea]. [Fecha de consulta: 3 de noviembre del 2020]. Disponible en:
https://www.matesfacil.com/ESO/probabilidad/conceptos-experimento-aleatorio-espacio-muestral-suceso-independiente-incompatible-contrario-ejemplos-test-moneda-bolas.html
-PROBABILIDADADES: REGLA DE LA SUMA : Ejercicios Resueltos [en línea]. [Fecha de consulta: 3 de noviembre del 2020]. Disponible en:
https://www.youtube.com/watch?v=yPXreAHcfJg





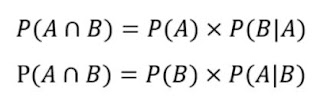






Comentarios
Publicar un comentario